劣モジュラ関数

劣モジュラ関数 (submodular function) とは，有限集合 $V$ の冪集合 $2^V$ 上で定義された関数 $\funcdoms{f}{2^V}{\setR \cup \set{+\infty}}$ であって，任意の $X, Y \subseteq V$ に対し，不等式 $$\begin{aligned} f(X) + f(Y) \ge f(X \cup Y) + f(X \cap Y) \end{aligned}$$ を満たすもののことをいい，具体例としては無向グラフのカット関数や集合族の被覆関数が有名です．同値な定義として，$X \subseteq Y$ を満たす任意の $X, Y \subseteq V$ と $x \in V \setminus X$ に対し， $$\begin{aligned} f(X \cup \set{x}) - f(X) \ge f(Y \cup \set{x}) - f(Y) \tag{1} \end{aligned}$$ を満たす関数としても特徴付けられます．不等式 (1) は「手元の集合が大きいほど，新たに要素を加えたときの効用の増分が下がる」という，経済学における限界効用逓減性を表しています． プリキュアで学ぶ劣モジュラ関数が大変分かりやすい入門記事として評判です．劣モジュラ関数は，多項式回の関数値オラクル呼び出しによって最小化可能であることが知られており [3, 5]，ある種の「離散版凸関数」のような存在として認識されています．

最小化可能な関数が与えられたとき，その最適解 1 つを構成して満足するのではなく，最適解全体の構造を保持したいと考えるのは自然でしょう．$X, Y \subseteq V$ を，$f$ を最小化する入力（最小化元）としたとき，上の不等式より，$X \cup Y$ および $X \cap Y$ もともに $f$ を最小化します．したがって，$f$ の最小化元全体の集合は $\cup$ と $\cap$ で閉じた $V$ の部分集合族となります．このような集合族を分配束 (distributive lattice) とよびます．台集合 $V$ のサイズを $n$ としたとき，$f$ の最小化元集合として現れる分配束は最大で $2^n$ 個の要素（部分集合）をもつので，最小化元すべてを愚直に保持するのは現実的ではありません． Birkhoff の表現定理 (Birkhoff’s representation theorem) によると，分配束の元のうち，（結び）既約元 (irreducible element) とよばれるいくつかの特別な元を保持すると，それらがなす半順序集合 (partially ordered set; poset) から元の分配束を完全に復元できるということが知られています．既約元の数は高々 $n$ であるため，この定理によって，劣モジュラ関数の最小化元集合の効率的表現が与えられます．

上記では，劣モジュラ関数 $f$ を $2^V$ 上に定義された関数（集合関数）として定めましたが，$V$ の部分集合 $X$ を $n$ 次元の 0-1 ベクトル $x$ と同一視することにより（特性ベクトル），$f$ を $\set{0, 1}^n$ 上の関数とみなすことができます．$\set{0, 1}^n$ 上の二項演算 $\join, \meet$ を，各 $x,y \in \set{0, 1}^n$ と $i = 1, \ldots, n$ に対して $\prn{x \join y}_i \defeq \max\{x_i, y_i\}$，$\prn{x \meet y}_i \defeq \min\{x_i, y_i\}$ と定めると，$X \leftrightarrow x, Y \leftrightarrow y$ という対応により, 不等式 (1)は $$\begin{aligned} f(x) + f(y) \ge f(x \join y) + f(x \meet y) \end{aligned}$$ と記述されます．

$k$-劣モジュラ関数

$k$ と $n$ を自然数とします．Huber–Kolmogorov [2] によって定義された $k$-劣モジュラ関数 ($k$-submodular function) とは，劣モジュラ関数の定義域を $\set{0, 1}^n$ から ${S_k}^n \defeq \set{0, 1, \ldots, k}^n$ に広げた関数です．ここで $S_k$ の元の大小関係は，以下のHasse 図で表現される半順序関係で定められます（$0$ が最小，$1$ から $k$ は互いに比較不能）．

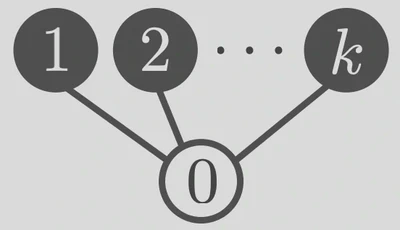
${S_k}^n$ の元 $x, y$ に対し，二項演算 $\sqcup, \sqcap$ を $$\begin{aligned} (x \sqcup y)_i &\defeq \begin{cases} \max\{x_i, y_i\} & (\text{$x_i$ and $y_i$ are comparable}), \\ 0 & (\text{$x_i$ and $y_i$ are incomparable}), \end{cases} \\ (x \sqcap y)_i &\defeq \begin{cases} \min\{x_i, y_i\} & (\text{$x_i$ and $y_i$ are comparable}), \\ 0 & (\text{$x_i$ and $y_i$ are incomparable}) \end{cases} \end{aligned}$$ と定義します．関数 $\funcdoms{f}{{S_k}^n}{\setR \cup \set{+\infty}}$ が $k$-劣モジュラ関数であるとは，任意の $x,y \in {S_k}^n$ に対し，不等式 $$\begin{aligned} f(x) + f(y) \ge f(x \sqcup y) + f(x \sqcap y) \end{aligned}$$ を満たすことをいいます．$k = 1$ のときは通常の劣モジュラ関数に，$k = 2$ のときは双劣モジュラ関数 (bisubmodular function) とよばれる関数に一致します．

$k$-劣モジュラ関数は，$k = 1, 2$ のときは多項式回の関数値オラクル呼び出しで最小化可能ですが，$k \ge 3$ の場合にそれが可能であるかどうかは重要な未解決問題となっています．具体例としては，マルチウェイカット問題のある種の緩和問題の目的関数や，それを拡張した Potts エネルギー関数，さらにより一般的には，基本$k$-劣モジュラ関数 (basic $k$-submodular function) とよばれる関数の非負結合として表現される関数 [4]が知られており，これらはいずれも最小カットを求めるアルゴリズムによって最小化することが可能です．

研究成果

劣モジュラ関数の場合と同様，$k$-劣モジュラ関数 $f$ の最小化元の集合は $\sqcup$ と $\sqcap$ で閉じた ${S_k}^n$ の部分集合となります．本研究の主結果は，このような ${S_k}^n$ の部分集合の特徴付けを与えたというものです．

まず，簡単な考察により， $\sqcup$ と $\sqcap$ で閉じた ${S_k}^n$ の部分集合 $\mathcal{L}$ はメディアン半束 (median semilattice) とよばれる構造をなすことが分かります．メディアン半束は分配束の一般化であり，Birkhoff の表現定理によって分配束と対応していた半順序集合は，非整合対付き半順序集合 (poset with inconsistent pairs; PIP) に拡張されることとなります [1]．すなわち，$\mathcal{L}$ の既約元全体 $P$ を集めてくると，$P$ は PIP をなし，さらに $P$ から元の $\mathcal{L}$ を完全に復元することができます．$\mathcal{L}$ のサイズは最大 ${(k+1)}^n$ ですが，$P$ のサイズは高々 $kn$ であることを示すことができ，これによって $f$ の最小化元集合のコンパクトな表現が与えられます．また，PIP はメディアン半束と一対一対応するものですが，すべてのメディアン半束が $k$-劣モジュラ関数の最小化元集合として現れるわけではないため，$\mathcal{L}$ に対応するコンパクト表現 $P$ はすべての PIP を取りうるわけではありません．本研究では，$P$ としてありうる PIP の部分クラスの特徴付けを与えました（初等的 PIP (elementary PIP) と名付けました）．

また，本研究では初等的 PIP を実際に構成するアルゴリズム的結果も与えています．まず，$k$-劣モジュラ関数 $f$（およびその制限）の最小化元を 1 つ返すオラクルが与えられたとき，それを複数回呼ぶことで，$f$ の最小化元全体を表現する初等的 PIP を構成する多項式時間アルゴリズムを与えました．加えて，前述の Potts エネルギー関数や，基本 $k$-劣モジュラ関数の非負結合に対し，より少ない計算時間で同様の初等的 PIP を出力するアルゴリズムも設計しました．Potts エネルギー関数は，画像処理におけるノイズ除去手法である「グラフカット」で使用されるものですが，実際にノイズ除去のインスタンスに対して提案アルゴリズムを適用し，目的関数の最小化元集合を観察するという実験も行いました．

参考文献

1. J.-P. Barthélemy and J. Constantin. Median graphs, parallelism and posets. Discrete Mathematics, 111(1–3):49–63, 1993.
2. A. Huber and V. Kolmogorov. Towards minimizing $k$-submodular functions. In Proceedings of the 2nd International Symposium on Combinatorial Optimization (ISCO 2012), LNCS 7422, pp. 451–462, 2012.
3. S. Iwata, L. Fleischer, and S. Fujishige. A combinatorial strongly polynomial algorithm for minimizing submodular functions. Journal of the ACM, 48(4):761–777, 2001.
4. Y. Iwata, M. Wahlström, and Y. Yoshida. Half-integrality, LP-branching and FPT algorithms. SIAM Journal on Computing, 45(4):1377–1411, 2016.
5. A. Schrijver. A combinatorial algorithm minimizing submodular functions in strongly polynomial time. Journal of Combinatorial Theory, Series B, 80(2):346–355, 2000.