離散最適化 (岩田教授)
離散 (組合せ) 最適化問題とは, 最適化問題の中でも特に「解が離散 (組合せ) 的な構造を持つもの」を指します. たとえば,
- 現在地から目的地までの最短経路を求める問題
- セールスマンが顧客先を回るための経路を設計する問題
- 双方に好みがある状況において学生の大学への割当を決める問題 などが挙げられます.
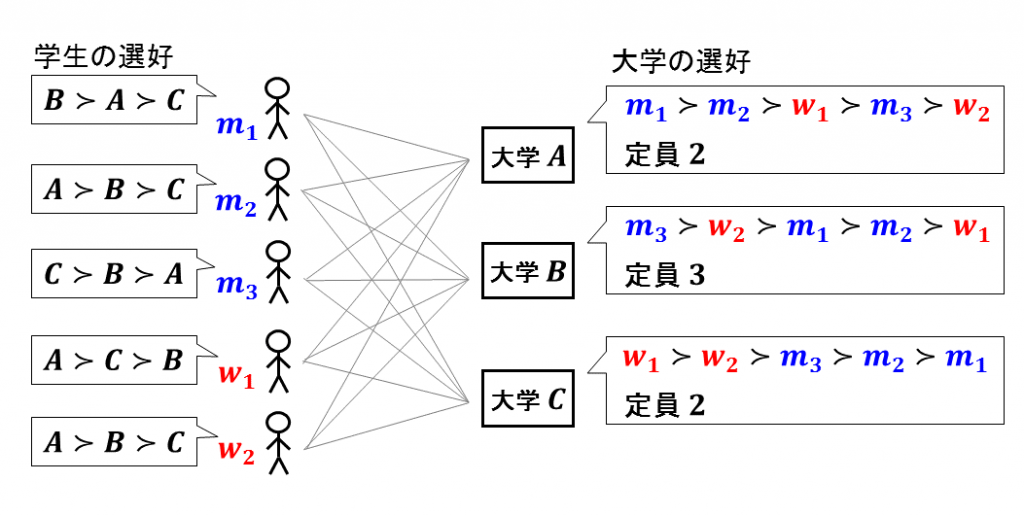
離散最適化問題の中には, その構造を利用して効率的に解くことのできる問題と, 効率的な厳密解法の開発は本質的に無理であろうと考えられている問題とがあります. 実用上有用な多くの離散最適化問題が, NP困難と呼ばれる後者の部類に属するとはいえ, 効率的に解くことのできる問題の構造を知ることは, 計算困難な問題に対する現実的な対処法を探る際の道具としても重要です. このような背景から, 離散最適化問題に対し, 問題の持つ構造の解析や, 問題に対する効率的なアルゴリズムの開発, および, 問題を統一的に扱えるような枠組みや理論の構築を目指しています.
固有値計算による大域最適化(岩田教授)
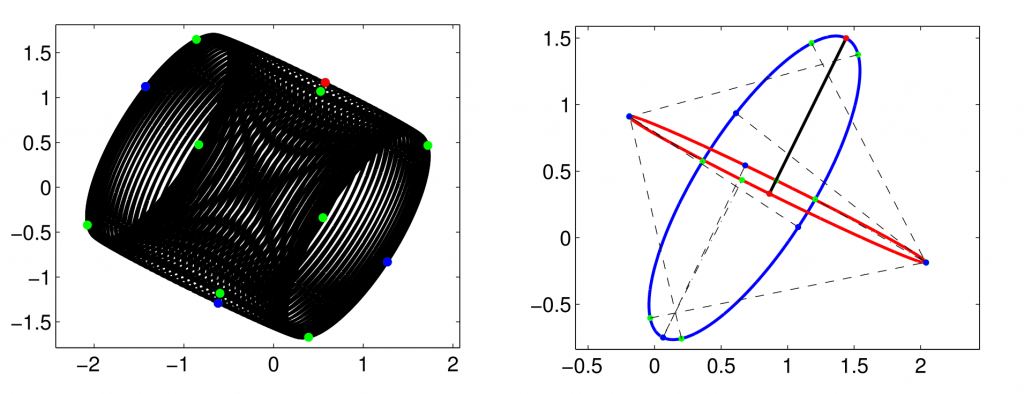
連続変数に関する最適化問題では,実行可能領域と目的関数の両方が凸である凸最適化問題を解く効率的なアルゴリズムが知られているのに対して,そうではない非凸最適化問題は,一般に難しいと言われています.しかし,幾何的な背景を有する特殊な非凸最適化問題に対しては,その構造を利用して効率的な厳密解法が設計できる可能性が残されています.下図では,一般化固有値問題を解いて,非凸最適化問題のKKT点を列挙することによって,楕円体間の符号付き距離を計算しています.一般化固有値計算による大域最適化は,数理7研が世界に先駆けて開発した新たな計算手法です.
離散幾何・計算幾何 (谷川准教授)
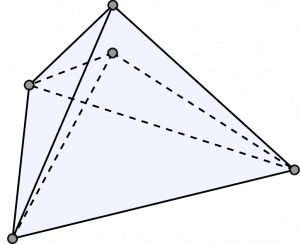
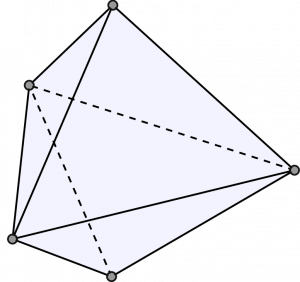
科学・工学の諸問題に現れる幾何的対象を計算機上で効率的に解析するための研究を行なっています.特にグラフの埋込問題や剛性問題を研究しています.例えば,指定された辺長を実現するようなグラフの平面描画は存在するか?存在するなら,可能な描画は唯一に定まるか?といった問題を考えています.また同様な問題を球面空間で考え,低階数行列補完問題などの研究も行っています. センサー間の距離情報から全体の配置を同定する問題や,タンパク質の挙動を推定する問題など,様々な応用を踏まえた理論展開を目指しています.

メカニズムデザイン・計算的社会選択理論・公平分割理論 (五十嵐准教授)
公平にケーキを分けるにはどのようにすれば良いでしょうか?社会選択理論とは,異なる好みを持つ人々に対して,適切に好みを集約する方法を数理的に解析する理論です.古くは政治学や経済学的な視点から研究されてきましたが,近年の情報技術の発展により計算論的側面からの研究が進みつつあります.

学習理論を用いたアルゴリズム設計 (坂上助教)
学習理論の観点から実問題の傾向に合わせたアルゴリズムを設計する研究しています.例えば「推薦システム内で二部グラフの最大重みマッチングを求めるアルゴリズムを用いて,何度もマッチングを計算する」といった応用の場面では,実際に解くべき問題の傾向に合わせて従来のアルゴリズムに手を加えることで,より良い性能が発揮されるということがしばしば起こります.実際,二部グラフのマッチングの場合については,十分なサイズの問題サンプル上で双対最適解を学習しウォームスタートすることで,理論的にも計算時間が短縮され得ることが,Dinitzらの最近の研究によって分かっています.
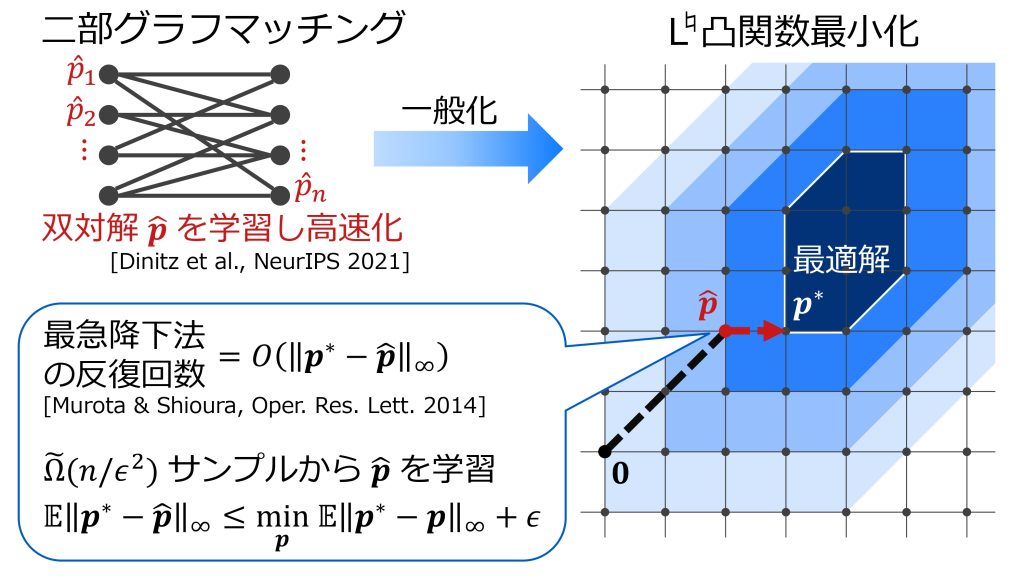
我々の研究では,DinitzらのアイデアをL/L♮凸関数最小化に対する最急降下法に拡張しました.離散凸解析の視点から見ることで「最適解に近い初期解を学習できれば問題が高速に解ける」という結果の自然な解釈が得られ,同様のアイデアをより幅広い問題(重み付きマトロイド交叉や画像処理における離散最適化問題など)に適用できるようになりました.この研究の他にも,グラフ探索や行列の低ランク近似などの様々な問題に対するアルゴリズムについて,機械学習の手法を取り入れて性能を向上するための研究を行っています.
線形代数と離散最適化 (大城助教)
グラフの全域木問題やマッチング問題など,グラフやその一般化であるマトロイド上のある種の離散最適化問題は,記号を含む行列の階数を計算する問題として表現できます.行列表現は線形計算による効率的な離散最適化手法を与えるとともに,解の個数の数え上げやサンプリングにも応用できます.私はこの離散最適化問題と行列表現の対応の拡張と応用に取り組んでいます.例えば,マッチング問題において,解が実数値を取れるように連続拡張した問題は,記号を代数的に「非可換」であるとみなした場合の行列の階数に対応するということを示しました.

また,電気回路網や化学反応系などのシステム解析で現れる行列に対して,離散最適化手法を用いて効率的に解析する手法も研究しています.例えば,線形微分方程式系や線形差分方程式系において,その解の自由度を決定する組合せ的手法を設計しました.