生命現象の最適モデリング
-
“先を読む”コウモリの三次元飛行経路計画
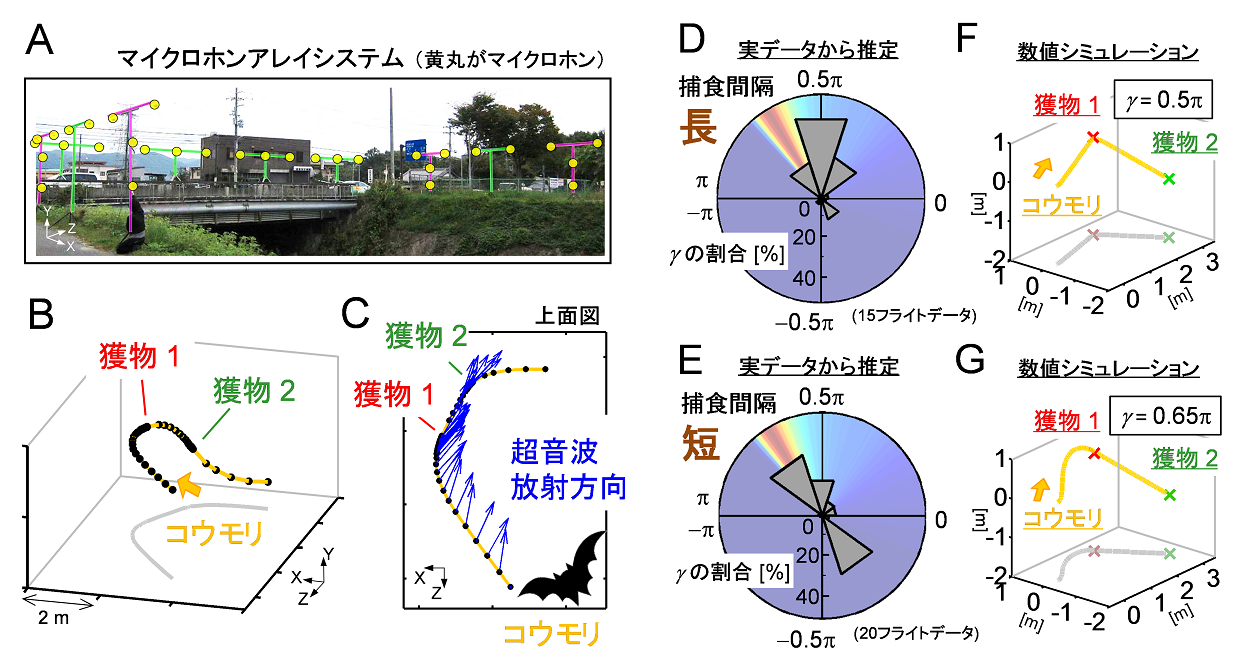
コウモリは高度に発達したソナーシステムを用いて,多くの微小な飛翔昆虫を飛びながら次々と捕食する.本研究では,野外実験と数理モデリングによって,コウモリが目の前の獲物だけでなく,その次の獲物に超音波ソナーによって注意を払い,双方の獲物を順次捕食するルートを飛行していることを明らかにした.今後,選択的注意機構に関する研究や,ドローンなどの自律移動ロボットの軌道計画研究分野における新しいモデル動物としての応用が期待できる.
以下の図は,野外での音響計測(A)で得られたコウモリの軌道の一例(B,C)と,軌道データから推定されたパラメータのヒストグラム(D,E)である.捕食時間間隔が長いときは目の前の獲物(獲物1)の情報のみに基づいた軌道が計画されていた(D,F)のに対して,捕食時間間隔が短いときは次の獲物(獲物2)の情報にも基づいて軌道が計画されており(E,G),捕食成功率を調べた数値計算の最適値(D,Eの赤色部分)とヒストグラムのピークが合致していることが分かる(E).
E. Fujioka, I. Aihara, M. Sumiya, K. Aihara and S. Hiryu: Echolocating bats use future-target information for optimal foraging, Proceedings of the National Academy of Sciences of the United States of America, vol. 113, pp. 4848-4852, 2016.
-
植物の概日時計に対する数理的解析
高次元の時系列データは多くのパラメータを用いて記述することが一般的であるが,重心座標による予測手法を利用することで少数のパラメータのみを用いた数理モデルを作成することができる.この数理モデルに基づいてシロイヌナズナの概日リズムを解析し,植物の概日リズムに器官ごとの階層性があり,茎頂がその頂点に位置することが明らかになった.
>>> 論文へのリンクはこちら
N. Takahashi, Y. Hirata, K. Aihara and P. Mas: A hierarchical multi-oscillator network orchestrates the Arabidopsis circadian system, Cell,
vol. 163, pp. 148-159, 2015.
微分代数方程式の最適モデリング
-
Kronecker標準形の解析とシステム制御への応用
微分代数方程式の数値的難しさを表す指標として,Kronecker指数が定義されている.微分代数方程式の最適モデリングでは,与えられた動的システムに対してKronecker指数の小さい微分代数方程式モデルを求めることが必要とされている.本研究では,Kronecker指数と関係の深いKronecker標準形をマトロイド理論的アプローチにより解析した.さらに,動的システムの可制御性解析への応用として,構造可制御部分空間の次元を効率的に計算する手法を提案した.
S. Iwata and M. Takamatsu: On the Kronecker canonical form of singular mixed matrix pencils, SIAM Journal on Control and Optimization,
vol. 55, pp. 2134-2150, 2017.
-
非線形微分代数方程式に対する組合せ的前処理手法
微分代数方程式 (DAE) の数値的な解きにくさは,指数とよばれる特性量によって特徴づけられる.DAE の数値解を精度良く得るためには,与えられた DAE を低指数の DAE に変換する指数減少が前処理として重要である.しかし,現在広く用いられている Mattsson–Söderlind の指数減少法(MS 法)は,ある種の DAE に対しては適用することができない.本研究では,記号計算と組合せ的手法を融合することで,MS 法が適用不能な非線形 DAE を適用可能な DAE に変換する 2 種類の前処理手法を提案した.提案手法を実装した MATLAB ライブラリはソフトウェアにて公開中である.
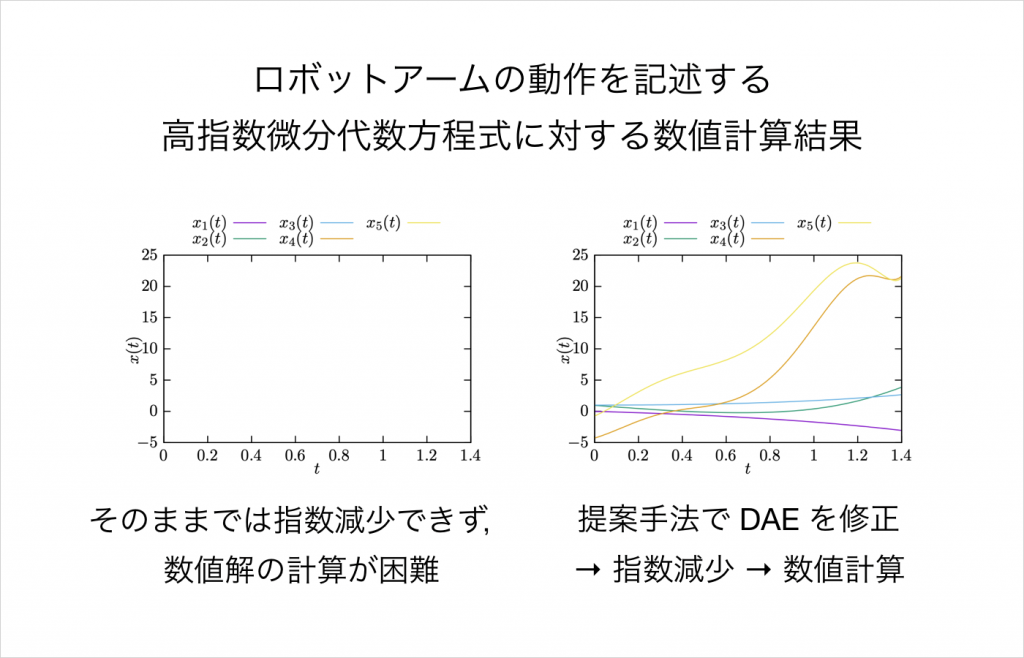
以下の図は,平面上のロボットアームの動作を記述する高指数 DAE(文献 [1] から引用)に対する数値計算結果を示している.この DAE は MS 法を適用することができず,そのままでは数値解の計算が困難である.提案手法を用いて MS 法が適用可能な DAE に修正することで,指数減少を経由して数値解を得ることができる.
- S. L. Campbell, E. Griepentrog. Solvability of general differential algebraic equations. SIAM Journal on Scientific Computing, 16(2):257–270, 1995.
T. Oki. Improved structural methods for nonlinear differential-algebraic equations via combinatorial relaxation. In Proceedings of the 44th International Symposium on Symbolic and Algebraic Computation (ISSAC ’19), pp. 315−322, 2019.
統計的モデルの最適化
-
統一的な2値判別モデルとその解法の提案
2値判別問題とは, 与えられたサンプルが2つのクラスのどちらに属するのかを予測する問題である. その予測に用いる判別関数の定め方を最適化問題として記述したものが2値判別モデルであり, サポートベクターマシンやロジスティック回帰をはじめとして多くのモデルが提案されている. 本研究では, 様々な2値判別モデルを扱いやすい形で統一的に定式化し, その定式化に対して汎用的かつ高速な解法を提案した. 数値実験では, 大規模インスタンスの計算時間に関して, 既存手法に対する提案手法の優位性を示すことができた. このように汎用性と高速さを兼ね備えた解法は, 複数のモデルの判別精度を比較し適切なモデルを選択する上で有用である.
N. Ito, A. Takeda and K.-C. Toh: A unified formulation and fast accelerated proximal gradient method for classification, Journal of Machine Learning Research, vol. 18, pp. 1-49, 2017.
ネットワーク現象の解析で得られる大量のデータを処理する手法に向けて
-
テンソルデータの圧縮アルゴリズム
テンソルのCP分解は交互最小残差法(ALS法)により近似分解を求めるのが主流であるが,大きなテンソルに対しては計算量が大きいという難点がある.3階テンソルに対しては巧妙なサイズ削減を用いたASD法が知られているが,動作がやや不安定であるという欠点がある.本研究では,ALSの安定性とASDの高速性を兼ね備えたアルゴリズム(reduced ALS法)を提案し,数値実験により有用性を示した.
以下の図は,ある男性の顔写真を10枚並べたデータをCP分解により圧縮したものである.Reduced ALS法は元の画像をある程度保持していることがわかる.

T. Murakoshi and T. Matsuo: A fast alternating least squares method for third-order tensors based on a compression procedure, JSIAM Letters, vol. 7, pp. 5-8, 2015.
-
行列の低ランク基底問題と画像分離への応用
ベクトル・行列における「疎・低ランク」な表現はデータ圧縮に有用である.本研究では,行列の低ランク基底を求めるアルゴリズムを提案し,本アルゴリズムの画像分離への応用を示した.
以下の図は,4枚の画像を低ランク行列で近似し混合してから,本アルゴリズムを用いて分離したものである.混ざった画像が正しく分離されていることが確認できる.

Y. Nakatsukasa, T. Soma and A. Uschmajew: Finding a low-rank basis in a matrix subspace, Mathematical Programming Series A, 2016.